Prose_随机森林方法的案例
最近学习了一些机器学习的传统分类算法。这里用传统分类树(ID3算法与CART算法)、条件推断分类树与随机森林算法,示例预测个人最终是否在体制内就业。基于2009年JSNET广州数据,通过R语言的"rpart"包、"party"包与"randomForest"包,最终模型的预测准确率在75%左右。但这一预测由于数据限制,难以厘清某些变量与就业的前后关系(如社会资本的影响),因此这一预测更应称为判断,未来可以进一步考虑因果预测机制。
(一)Classification Tree
R语言中分类树模型最常用的是"rpart"包与"party"包。这里同时用两个包进行分类树模型预测。对于它们的原理,很多文章已经讲得十分清楚。
“rpart"包的处理方式不同于"party"包,它首先对所有自变量和所有分割点进行评估,最佳的选择是使分割后组内的数据更为"一致”(pure)。这里的"一致"是指组内数据的因变量取值变异较小。“rpart"包对这种"一致"性的默认度量是Gini值。但确定停止划分的参数仍有很多(参见rpart.control),这些参数是非常重要且微妙的,因为划分越细,模型越复杂,越容易出现过度拟合的情况,而划分过粗,又会出现拟合不足。处理这个问题通常是使用"剪枝”(prune)方法。即先建立一个划分较细较为复杂的树模型,再根据交叉检验(Cross-Validation)的方法来估计不同"剪枝"条件下,各模型的误差,最后选择误差最小的树模型。
由于"rpart"包处理缺失值很麻烦,这里首先将最终涉及的变量:是否体制内就业、社会资本、户口、年龄、教育、是否为党员,这六个变量的缺失值予以省略,进入决策树分析的样本量为915个。我们首先设定随机数为"1234",通过放回随机抽样将总样本按30%与70%分为两个部分,即训练组(Train data)670个与测试组(Test data)245个。目前较为流行的分类树算法有ID3算法、C4.5算法与CART算法,因为C4.5算法使用信息增益率作为不纯度,是对ID3算法使用信息增益作为不纯度的改进,所以我们仅使用ID3作为示例;而CART算法使用基尼系数作为不纯度,不同于ID3与C4.5,因此我们最终使用ID3算法与CART算法。
1 | # set train test |
我们首先使用传统的ID3算法,通过"maptree"包,我们得到训练组分类树结果。
1 | ## (1) id3 train |
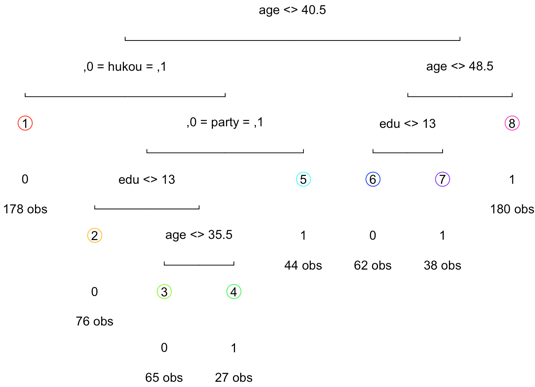 Fig.1 id3 classification tree
Fig.1 id3 classification tree进一步,为了评估这一训练模型的好坏,我们查看模型的误差与参数复杂度(complexity parameter,下文简称为CP)。通过CP可以看到,当nsplit为7的时候,即有八个叶子结点的树,要比nsplit为5,即六个叶子结点的树的交叉误差要小;进一步我们调用CP与xerror的相关图,也显示这一模型不需要进行剪枝。我们使用ID3算法训练出的决策树模型就测试组进行预测,构建混淆矩阵表,预测准确率为0.722449。
CP作为控制树规模的惩罚因子,简言之,CP越大,树的分裂规模(nsplit)越小。输出参数(rel error)则指示了当前分类模型树与空树之间的平均偏差比值;xerror为交叉验证误差,xstd为交叉验证误差的标准差。决策树剪枝的目的就是为了得到更小交叉误差(xerror)的树。
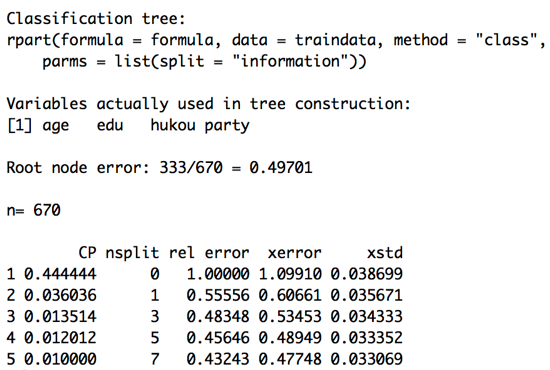 Fig.2 id3 cp
Fig.2 id3 cp  Fig.3 id3 cperror
Fig.3 id3 cperror使用CART算法,通过"maptree"包,我们得到训练组分类树结果。为了评估这一训练模型的好坏,我们查看模型的误差与CP,可见,图略。当nsplit为5的时候,即有六个叶子结点的树,要比nsplit为4,即五个叶子结点的树的交叉误差要大;进一步我们调用CP与xerror的相关图,均显示这一模型需要进行剪枝。因此,我们选择xerror最小时候对应的CP值来剪枝,即CP为4时,我们得到新的决策树模型,CART决策树的训练组剪枝后划分结果。继而观察改进后的CP与xerror相关图,可以认为不再需要剪枝。
我们使用CART算法训练出的剪枝后决策树模型就测试组进行预测,构建混淆矩阵表,预测准确率为0.7387755,这一准确率好于ID3算法训练出的决策树模型预测准确率0.722449。
1 | ### 使用ID3算法时候, split = 'information' ,使用CART算法的时候, split = 'gini' |
我们继续使用"party"包,使用条件推断决策树进行预测,训练组的预测成功率为0.7686567。得到推断决策树的训练组划分结果。进而,我们将训练出决策树模型就测试组进行预测,构建混淆矩阵表,预测准确率为0.7102041。但这一预测效果不如传统CART算法的0.7387755。
“party"包的背景理论是"条件推断决策树”(conditional inference trees),不同于传统决策树"rpart"包,它是根据统计检验来确定自变量和分割点的选择,即先假设所有自变量与因变量均独立;再对它们进行卡方独立检验,检验P值小于阀值的自变量加入模型,相关性最强的自变量作为第一次分割的自变量。自变量选择好后,用置换检验来选择分割点。用"party"包建立的决策树不需要剪枝,因为阀值就决定了模型的复杂程度。所以如何决定阀值参数是非常重要的(参见ctree_control)。较为流行的做法是取不同的参数值进行交叉检验,选择误差最小的模型参数。
1 | # Conditional Inference Tree |
(二)Random Forest
尽管我们上述比较了传统ID3、CART算法与新近的条件推断决策树,但一棵树的生成肯定还是不如多棵树,随机森林结构比较复杂,但是它却极端易用,需要的假设条件(如变量的独立性、正态性等)比逻辑斯蒂回归等模型要少得多,也不需要检查变量的交互作用和非线性作用是否显著,在大多数情况下模型参数的缺省设置可以给出最优或接近最优的结果。
因此为了解决单个决策树泛化能力弱的缺点,我们可以使用基于"rpart"包的随机森林"randomForest"包。我们设定生成100棵决策树,进行随机森林的预测。随机森林的训练组预测准确率为0.7641791。我们进一步计算MeanDecreaseGini值,该数值即通过基尼指数计算每个变量对分类树上每个节点的观测值的异质性影响,值越大表示该变量的重要性越大。年龄(其MeanDecreaseGini值为105.03092)、社会资本(其MeanDecreaseGini值为68.44540)与户口(其MeanDecreaseGini值为34.15491)对个人最终是否体制内就业有显著影响。
1 | # random forest |
最后,我们基于训练组模型,对测试组进行预测的准确率为0.7265306。本文随后进行了多次测试,准确率最终稳定在75%左右。认为该模型可以大致预测个人最终的就职情况。但值得注意的是,由于数据限制,我们很难完全厘清某些变量如社会资本对个人就职的影响,是个人就职影响社会资本,还是反过来社会资本影响个人就职。因此这里的示例仍更偏向于判断而非预测。