Prose_用ARIMA做人口预测

有关人口预测的模型和方法很多，不同方法和模型各有优缺点，这里用ARIMA模型与2019年某市统计年鉴示例常住人口的预测。ARIMA(p,d,q)，p 为自回归阶数，d为时间序列称为平稳序列进行差分的阶数，q为移动平均阶数，其一般表达式为：

$$y_{1} = \mu + \varphi_{1}y_{t - 1} + \cdots + \varphi_{p}y_{t - p} + \theta_{1}\alpha_{t - 1} + \cdots + \theta_{q}\alpha_{t - q}$$

1．预测参数设定与估计

运用 ARIMA 模型建立模型通常从以下三个步骤出发：
第一步，时间序列平稳化处理:根据时间序列趋势图，如果所得出的时间序列不是平稳时间序列，应当采用差分运算将原时间序列变为平稳时间序列，几阶差分需要通过单方根检验得出最优差分阶数d。差分运算就是后一时间点减去当前时间如$y_{t}-y_{t-1}$，用D表示，定义为$D_{y_{t}}=y_{t}-y_{t-1}$。那么k阶差分可表示为：$y_{t}-y_{t-\mathrm{k}}=D_{k} y_{t}=\left(1-L^{k}\right) y_{t}=y_{t}-L^{k} y_{t}$，$L$为滞后算子，定义为$L_{y_{t}}=y_{t-1}$，则k阶之后算子定义为$L^{k} y_{t}=y_{t-k}$。
第二步，模型参数估计与检验：根据时间序列的自相关函数图(ACF)与偏相关函数图(PACF)的拖尾与截尾的性质，可以判断参数p与q。通过由低阶到高阶的尝试，选取最优的模型参数值；并进行残差的白噪声检验，选择合适的模型；如果未通过检验，应当重新选择模型。

	AR(p)	MA(q)	ARMA(p,q),p>0,q>0
ACF	拖尾	滞后q阶后截尾	拖尾
PACF	滞后p阶后截尾	拖尾	拖尾

具体而言，当d=0,ARIMA(p,d,q)模型实际上就是ARMA（p,q）模型；当p=0,ARIMA(0,d,q)模型可以简记为IMA（d,q）模型；当q=0,ARIMA(p,d,0)模型可以简记为ARI（d,q）模型；当d=1,p=q=0时，ARIMA（0，1，0）模型为游走模型或称醉汉模型，是最简单的ARIMA模型。
第三步，模型预测：运用选择的适当的ARIMA 模型对未来某市常住人口人数进行预测并分析。

2．人口预测主要结果

根据预测，2019至2025年，某市常住人口、在业人口及第二、三产业在业人口的主要数据如图所示。

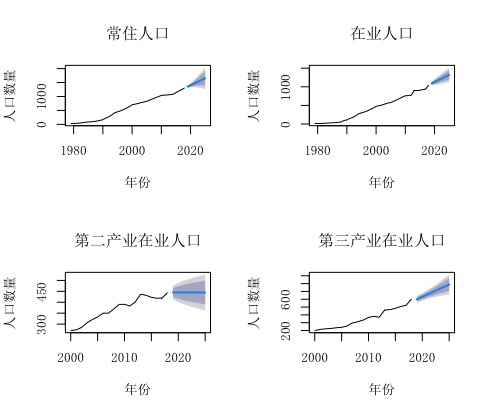
以常住人口为例，具体数据如下：
1979年至2018年某市常住人口人数如图左侧第一幅图所示，趋势图显示1979年至2018年某市常住人口总体呈上升趋势。
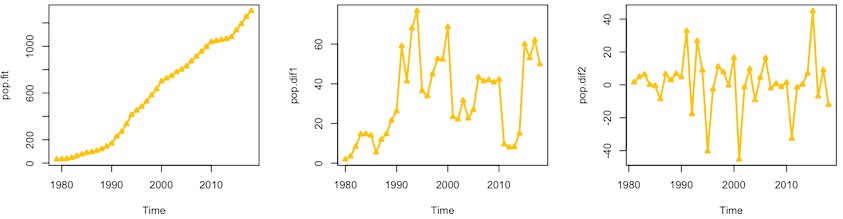
由于某市常住人口的时间序列有明显的递增趋势，所以它一定不是平稳序列，因此将原始数据进行差分运算。进行差分遵循从小到大这一特点，故现对该时间序列进行1阶差分运算，得出如图左侧第二幅图所示的趋势图。1阶差分时间序列图显示，1阶差分处理后的数据增减趋势趋于平稳，但基于R语言可以迅速得出，常住人口1阶差分的ADF检验P值大于0.05，差分1次后的时间序列仍非平稳序列，依据数据最优化及准确性原则，对1阶差分后的时间序列再做一次差分运算，常住人口2阶差分的ADF检验P值小于0.05，因此参数d取值为2。

library('tseries')
library('fUnitRoots')
pop <- read.xlsx("predict_shenzhen.xlsx", sheetName = "sheet1", encoding = 'UTF-8')
par(mfrow=c(1,3))
plot(pop.fit,col=7,pch=2,lwd=2,type="o")
# acf(pop.fit,lwd=2,col=4)
adf.test(pop.fit) #tseries
adfTest(pop.fit) #fUnitRoots
pop.dif1=diff(pop.fit,difference=1)
plot(pop.dif1,col=7,pch=2,lwd=2,type="o")
# acf(pop.dif1,lwd=2,col=4)
adf.test(pop.dif1)
adfTest(pop.dif1)
pop.dif2=diff(pop.fit,difference=2)
plot(pop.dif2,col=7,pch=2,lwd=2,type="o")
adf.test(pop.dif2)
adfTest(pop.dif2) #d=2

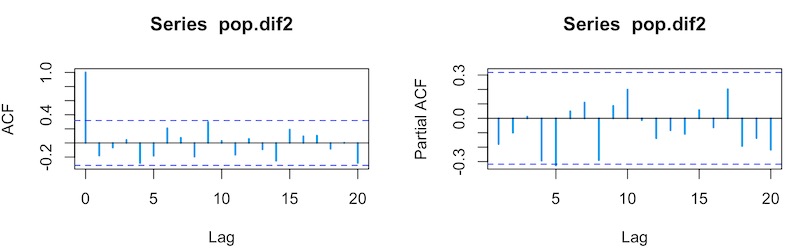
根据图“二阶差分后的自相关图与偏自相关图”，显示没有超过边界值。对平稳后的时间序列，即对1阶与2阶差分处理后的时间序列绘制自相关图与偏自相关图。

par(mfrow=c(1,2))
acf(pop.dif2,lwd=2,col=4,lag.max=20) 
pacf(pop.dif2,lwd=2,col=4,lag.max=20) # q=0 p=0
auto.arima(pop.fit,d=2,trace=T)

此时选择ARIMA(p,d,q)模型进行预测时，参数根据0、1、2从低阶到高阶选择，根据AIC准则作为选择最优值模型（表 某市常住人口ARIMA备选模型拟合统计量），比较发现模型ARIMA(0,2,0)的AIC=323.46最小，即此模型拟合效果最好。对残差序列进行白噪声检验，得出P值大于0.05，残差序列白噪声检验说明模型显著。判断ARIMA(0,2,0)模型对常住人口的时间序列拟合成功。

	ARIMA(2,2,2)	ARIMA(0,2,0)	ARIMA(1,2,0)	ARIMA(0,2,1)	ARIMA(1,2,1)
AICc	329.6454	323.4607	324.5957	324.3949	324.4877

运用上述得到的ARIMA(0,2,0)模型对某市常住人口及置信水平分别为80%和95%双层置信区间进行预测，得到下表。

pop.fit2=arima(pop.fit,order=c(0,2,0),method="ML")
pop.fit2
# white noise test
par(mfrow=c(1,1))
qqnorm(pop.fit2$residual)
qqline(pop.fit2$residual)
for(i in 1:3) print(Box.test(pop.dif2,type="Ljung-Box",lag=6*i))

最后，有80%的把握，2025年常住人口落入1399.77万人至1903.17万人区间内；有95%的把握，2025年常住人口落入1266.53万人至2036.41万人区间内。

pop.fore=forecast(pop.fit2,h=7) # Forecast
pop.fore

	预测值	80%置信区间	95%置信区间
2019	1352.49	1331.22,1373.76	1319.96,1385.02
2020	1402.32	1354.75,1449.89	1329.57,1475.07
2021	1452.15	1372.56,1531.75	1330.42,1573.88
2022	1501.98	1385.47,1618.50	1323.79,1680.17
2023	1551.81	1394.05,1709.57	1310.54,1793.09
2024	1601.64	1398.71,1804.57	1291.29,1911.99
2025	1651.47	1399.77,1903.17	1266.53,2036.41

另，统计数据的口径时常让人困扰。仅本文所使用的数据而言：（1）经普和年鉴的二、三产业占比的存在出入。如经普里2004到2008的二产业占比下降仅0.1%，但年鉴里下降3%；再如经普和年鉴2008、2013的二产业占比差异6%和8%（近10%）。（2）经普和年鉴的就业人口出入。经普2004、2008就业人口都比年鉴少；2013、2018就业人口比年鉴多。为了更贴近真实情况，可能是就业人口数据按经普2013、2018调整，然后平滑2008至2018的十年数据，但是具体占比仍按年鉴，这样做在整体就业人口上出入小，只影响二、三产业的人口数量。